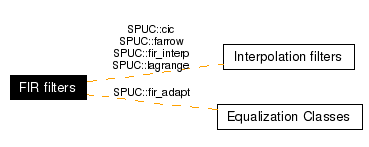
Main Page | Modules | Namespace List | Class Hierarchy | Alphabetical List | Class List | Directories | File List | Namespace Members | Class Members | File Members

FIR filters

Collaboration diagram for FIR filters:


Classes

class  SPUC::rfir< Numeric >
 template class rfir FIR filter implementation with complex input and real coefficients More...
class  SPUC::cic
 class for CIC digital filter More...
class  SPUC::farrow< Numeric >
 Template Class for Farrow implementation of a ploynomial interpolation using a FIR filter. More...
class  SPUC::fir< Numeric >
 Template Class for Modeling a Finite Impulse Response filter. More...
class  SPUC::fir_adapt< Numeric >
 template class fir_adapt Based on FIR class, created to support LMS adaptive filtering More...
class  SPUC::fir_decim< Numeric >
 template class fir_decim based on FIR class, created to support polyphase FIR decimation More...
class  SPUC::fir_interp< Numeric >
 template class fir_decim based on FIR class, created to support polyphase FIR interpolation More...
class  SPUC::fir_multi_interp< Numeric >
 template class fir_decim based on FIR class, created to support polyphase FIR interpolation More...
class  SPUC::fir_sparse_coef< Numeric >
 template class fir_decim based on FIR class, created to support spare coefficients (zero padded) More...
class  SPUC::lagrange< Numeric >
 Template Class for Lagrange interpolation using a FIR filter. More...
class  SPUC::remez_fir
 template remez FIR class More...
class  SPUC::running_average< Numeric >
 template class running average filter consisting of a delay line, adder and subtractor More...
class  SPUC::running_sum< Numeric >
 template class running average filter consisting of a delay line, adder and subtractor More...
class  SPUC::sum_and_dump
 sum and dump filter More...
class  SPUC::scic
 Registers are signed long and default number of stages is 2. More...

Functions

void SPUC::root_raised_cosine (fir< long > &rcfir, double alpha, int rate)
void SPUC::root_raised_cosine (fir< complex< long > > &rcfir, double alpha, int rate, int bits=10)
void SPUC::root_raised_cosine (fir< complex< long > > &rcfir, double alpha, int rate, int bits=10, double scale=1.0)
void SPUC::root_raised_cosine (fir< complex< double > > &rcfir, double alpha, int rate)
void SPUC::root_raised_cosine (fir_interp< complex< double > > &rcfir, double alpha, int rate)
void SPUC::root_raised_cosine (fir< double > &rcfir, double alpha, int rate)
void SPUC::raised_cosine (fir< long > &rcfir, double alpha, int rate)
void SPUC::raised_cosine (fir< double > &rcfir, double alpha, int rate)
double SPUC::io (double x)
 bessel function for kaiser window
void SPUC::hamming (double *w, long nf, double alpha, double beta)
 hamming window 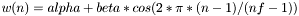$ w(n) = alpha + beta*cos( 2*\pi*(n-1)/(nf-1) )$
void SPUC::hanning (double *w, long nf)
 hanning window 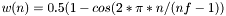$ w(n) = 0.5( 1 - cos( 2*\pi*n/(nf-1) )$
void SPUC::blackman (double *w, long nf)
 Blackman Window $ w[x] = 0.42 - 0.5*cos(2*\pi*x/nf) + 0.08*cos(2*\pi*x/nf)$.
void SPUC::kaiser (double *w, long nf, double beta)
 kaiser window
void SPUC::chebc (double nf, double dp, double df, double n, double x0)
 chebyshev window subroutine to generate chebyshev window parameters when one of the three parameters nf,dp and df is unspecified
void SPUC::cheby (double *w, long nf, long n, long ieo, double dp, double df, double x0)
 dolph chebyshev window design
void SPUC::butterworth_fir (fir< double > &butfir, double spb)
 calculates the sampled butterworth (max flat) filter impulse response
void SPUC::create_remez_lpfir (fir< double > &remezfir, double *edge, double *fx, double *wtx)
 calculates the coefficients for lowpass FIR based on Remez constraints
void SPUC::gaussian_fir (fir< double > &gaussf, double bt, double spb)
 calculates the sampled Gaussian filter impulse response
void SPUC::ls_fir (fir< double > fil, double fc, double spb)
 calculates the least square filter impulse response

Function Documentation

void SPUC::blackman (  double *  w,
long  nf
) 
 

Blackman Window $ w[x] = 0.42 - 0.5*cos(2*\pi*x/nf) + 0.08*cos(2*\pi*x/nf)$.

void SPUC::butterworth_fir (  fir< double > &  butfir,
double  spb
) 
 

calculates the sampled butterworth (max flat) filter impulse response

With B(p) the butterworth response we have:

$ B(p) = \displaystyle\sum_{k=1}^{N/2} \frac{\lambda(k)*(1+\alpha(k)*p/wc)}{1+2*cos(\beta(k))*p/wc + (p/wc)^2)}.$

with

N = Order of Butterworth filter (always even)

$ \beta(k) = (2 * k - 1) / (2 * N) k = 1, 2, .. N/2 $

$ \alpha(k) = sin((N/2 - 1) * \beta(k)) / sin(N * \beta(k) / 2) $

$ \lambda(p) = \frac{\sin(N*\beta(k)/2)}{sin(\beta(k))}. \displaystyle\prod_{m=1,m!=k}^{N/2} 2*cos(\beta(k) - cos(\beta(m))) $

The impulse response of B(p) can be found by realizing that:

$ \frac{p+a}{(p+a)^2 + w^2} <-> e^{-at} * cos(w*t) $

$ \frac{w}{(p+a)^2 + w^2} <-> e^{-at} * sin(w*t) $

and that B(p) can be written as a linear combination of the these two expressions:

$ \frac{x*(p+a)+y*w}{(p+a)^2 + w^2} <-> e^{-at}*x*cos(w*t) + y* sin(w*t) $

We find after some algebra:

$ x(k) = \alpha(k) $

$ w(k) = \sqrt{1 - cos(\beta(k)) * cos((\beta(k)))} $

$ a(k) = cos(\beta(k)) $

$ y(k) = (1 - \alpha(k) * cos(\beta(k)) / w(k) $

Also used is the time scaling rule for Fourier transforms: |a| * y(at) <--> Y(f/a)

void SPUC::chebc (  double  nf,
double  dp,
double  df,
double  n,
double  x0
) 
 

chebyshev window subroutine to generate chebyshev window parameters when one of the three parameters nf,dp and df is unspecified

void SPUC::cheby (  double *  w,
long  nf,
long  n,
long  ieo,
double  dp,
double  df,
double  x0
) 
 

dolph chebyshev window design

parameters

  • nf = filter length in samples
  • w = window array of size n
  • n = half length of filter = (nf+1)/2
  • ieo = even-odd indicator--ieo=0 for nf even
  • dp = window ripple on an absolute scale
  • df = normalized transition width of window
  • x0 = window parameter related to transition width
  • xn = nf-1

void SPUC::create_remez_lpfir (  fir< double > &  remezfir,
double *  edge,
double *  fx,
double *  wtx
) 
 

calculates the coefficients for lowpass FIR based on Remez constraints

void SPUC::gaussian_fir (  fir< double > &  gaussf,
double  bt,
double  spb
) 
 

calculates the sampled Gaussian filter impulse response

void SPUC::hamming (  double *  w,
long  nf,
double  alpha,
double  beta
) 
 

hamming window $ w(n) = alpha + beta*cos( 2*\pi*(n-1)/(nf-1) )$

void SPUC::hanning (  double *  w,
long  nf
) 
 

hanning window $ w(n) = 0.5( 1 - cos( 2*\pi*n/(nf-1) )$

double SPUC::io (  double  x  ) 
 

bessel function for kaiser window

:

function: io

void SPUC::kaiser (  double *  w,
long  nf,
double  beta
) 
 

kaiser window

void SPUC::ls_fir (  fir< double >  fil,
double  fc,
double  spb
) 
 

calculates the least square filter impulse response

void SPUC::raised_cosine (  fir< double > &  rcfir,
double  alpha,
int  rate
) 
 

void SPUC::raised_cosine (  fir< long > &  rcfir,
double  alpha,
int  rate
) 
 

void SPUC::root_raised_cosine (  fir< double > &  rcfir,
double  alpha,
int  rate
) 
 

void SPUC::root_raised_cosine (  fir_interp< complex< double > > &  rcfir,
double  alpha,
int  rate
) 
 

void SPUC::root_raised_cosine (  fir< complex< double > > &  rcfir,
double  alpha,
int  rate
) 
 

void SPUC::root_raised_cosine (  fir< complex< long > > &  rcfir,
double  alpha,
int  rate,
int  bits = 10,
double  scale = 1.0
) 
 

void SPUC::root_raised_cosine (  fir< complex< long > > &  rcfir,
double  alpha,
int  rate,
int  bits = 10
) 
 

void SPUC::root_raised_cosine (  fir< long > &  rcfir,
double  alpha,
int  rate
) 
 

Generated on Fri Sep 16 11:06:54 2005 for spuc by  doxygen 1.4.4